calcs.c File Reference

Core calculations for fractal rendering. More...

#include "fractol.h"

Include dependency graph for calcs.c:

Go to the source code of this file.

Functions
void	calculate_scales_and_limits (t_render_vars *vars, t_data *data)
	Calculates the scales and starting points for the fractal rendering.
int	precompute_coords (double **c_re, double **c_im, t_render_vars *vars)
	Precomputes the coordinates for each pixel in the fractal.
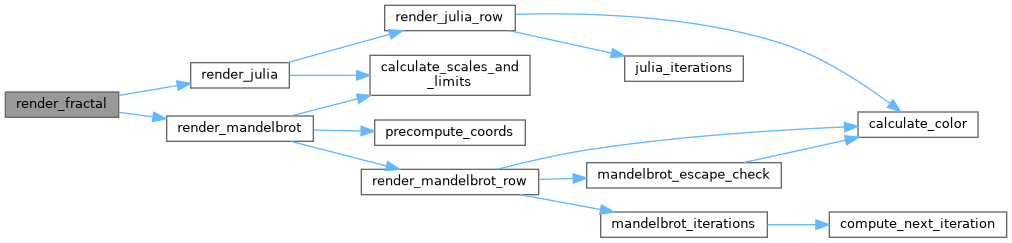
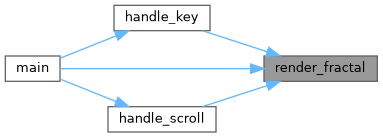
void	render_fractal (t_data *data)
	Renders the chosen fractal on the screen.
int	calculate_color (int iterations)
	Calculates the color of a pixel based on how many iterations it takes to "escape".

Detailed Description

Core calculations for fractal rendering.

This file contains the functions responsible for performing the core calculations required to render fractals. It handles:

• Scaling and positioning the fractal within the rendering window.
• Precomputing the coordinates ffor each pixel to optimize rendering performance.
• Rendering the fractal by delegating to specific algorithms (Julia or Mandelbrot).

• Mapping iteration counts to colors for visually representing fractal complexity.

  For non-technical users:

  • This file performs the "math magic" that powers the fractal visuals, calculating where and howw the fractal is drawn and colored on the screen.

Definition in file calcs.c.

Function Documentation

calculate_color()

int calculate_color

(

int

iterations

)

Calculates the color of a pixel based on how many iterations it takes to "escape".

Calculates the color based on the number of iterations.

This function determines the color of each pixel in the fractal by mapping the iteration count (how many steps we are needed to reach a threshold) to a color gradient.

For non-technical users:

• The function decides the color of each pooint in the fractal, creating the beautiful patterns you see based on how "complex" the point is.

Parameters

iterations

Number of iterations required for the opint to "escape".

Returns

Returns the calculated color as an integer.

Definition at line 131 of file calcs.c.

{
    double  it_count;
    int     base_gray;
    t_color color;
 
    it_count = (double)iterations / MAX_ITERATIONS;
    base_gray = (30 + 190 * (it_count * (1 - 0.2 * it_count)));
    color.r = base_gray - (5 * (1 - it_count) * it_count * it_count);
    color.g = base_gray - (10 * (1 - it_count) * (1 - it_count));
    color.b = base_gray - (15 * (1 - it_count) * it_count);
    return ((0xFF << 24) | (color.r << 16) | (color.g << 8) | color.b);
}

Here is the caller graph for this function:

calculate_scales_and_limits()

void calculate_scales_and_limits	(	t_render_vars *	vars,
		t_data *	data
	)

Calculates the scales and starting points for the fractal rendering.

Calculates scales and limits for rendering fractals.

This function determines how the fractal is scaled and positioned on the screen. It computes the scale factors for each pixel and establishes the starting points ffor the real and imaginary part of the fractal based on the zoom level and offsets.

For non-technical users:

• Think of it as setting the "zoom" and "pam" for the fractal to display it correctly on the screen.

Parameters

vars	Pointer to the rendering variables structure.
data	Pointer to the main data structure containing fractal information.

Definition at line 52 of file calcs.c.

{
    vars->scale[SCALE_X] = 4.0 / (WIDTH * data->zoom);
    vars->scale[SCALE_Y] = 4.0 / (HEIGHT * data->zoom);
    vars->start[COMPLEX_RE] = -2.0 / data->zoom + data->offset[OFFSET_X];
    vars->start[COMPLEX_IM] = -2.0 / data->zoom + data->offset[OFFSET_Y];
    vars->pixels = (uint32_t *)data->img->pixels;
}

Here is the caller graph for this function:

precompute_coords()

int precompute_coords	(	double **	c_re,
		double **	c_im,
		t_render_vars *	vars
	)

Precomputes the coordinates for each pixel in the fractal.

Precomputes coordinates for fractal rendering.

This function calculates the real and imaginary parts of the fractal for each pixel on the screen, storing them in arrays for quick access during rendering. It ensures that every point is prepared for the fractal calculations.

For non-technical users:

• Imagine this as creating a "grid" of points where the fractal will be drawn. This points tell the program where to caalculate the colors.

Parameters

c_re	Pointer to the array storing real coordinates.
c_im	Pointer to the array storing imaginary coordinates.
vars	Pointer to the rendering variables structure.

Returns

Returns 1 on success, or 0 if memory allocation fails.

Definition at line 78 of file calcs.c.

{
    int i;
 
    *c_re = (double *)malloc(WIDTH * sizeof(double));
    *c_im = (double *)malloc(HEIGHT * sizeof(double));
    if (!(*c_re) || !(*c_im))
        return (free(*c_re), free(*c_im), 0);
    i = -1;
    while (++i < WIDTH)
        (*c_re)[i] = vars->start[COMPLEX_RE] + i * vars->scale[SCALE_X];
    i = -1;
    while (++i < HEIGHT)
        (*c_im)[i] = vars->start[COMPLEX_IM] + i * vars->scale[SCALE_Y];
    return (1);
}

Here is the caller graph for this function:

render_fractal()

void render_fractal

(

t_data *

data

)

Renders the chosen fractal on the screen.

Render the specified fractal.

This function selects the appropiate rendering algorithm based on the fractal type chosen by the user (Julia or Mandelbrot) and renders it on the screen.

For non-technical users:

• Depending on the type of fractal (Julia or Mandelbrot), this function draws the chosen fractal pattern for you to see.

Parameters

data	Pointer to the main data structure containing fractal and rendering details.

Definition at line 108 of file calcs.c.

{
    if (data->fractal_type == JULIA)
        render_julia(data);
    else if (data->fractal_type == MANDELBROT)
        render_mandelbrot(data);
}

Here is the call graph for this function:

Here is the caller graph for this function: