fractol.h File Reference

#include "MLX42/MLX42.h"
#include <limits.h>
#include <stdlib.h>

Include dependency graph for fractol.h:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Data Structures
struct	s_color
	Represents an RGB color. More...
struct	s_data
	Data structure for fractal rendering. More...
struct	s_render_vars
	Variables used for fractal rendering calculations. More...
struct	s_atod_data
	Helper structure for string-to-double conversion. More...

Macros
#define	WIDTH   800
#define	HEIGHT   WIDTH
#define	ZOOM_IN   1.1
#define	ZOOM_OUT   0.9
#define	FRACTAL_LIMIT   4.0
#define	MAX_ITERATIONS   75
#define	RESET   "\033[0m"
#define	LIGHT_RED   "\033[38;5;203m"
#define	LIGHT_GOLD   "\033[38;5;220m"
#define	LIGHT_GREEN   "\033[38;5;120m"

Typedefs
typedef enum e_fractal_type	t_fractal_type
typedef enum e_offset_index	t_offset_index
	Indices for offsets in the x and y directions.
typedef enum e_scale_index	t_scale_index
	Indices for scaling factors in the x and y directions.
typedef enum e_complex_index	t_complex_index
	Indices for complex numbers (real and imaginary)
typedef enum e_number_flags	t_number_flags
	Flags for validating numbers.
typedef struct s_color	t_color
	Represents an RGB color.
typedef struct s_data	t_data
	Data structure for fractal rendering.
typedef struct s_render_vars	t_render_vars
	Variables used for fractal rendering calculations.
typedef struct s_atod_data	t_atod_data
	Helper structure for string-to-double conversion.

Enumerations
enum	e_fractal_type { MANDELBROT , JULIA }
enum	e_offset_index { OFFSET_X , OFFSET_Y }
	Indices for offsets in the x and y directions. More...
enum	e_scale_index { SCALE_X , SCALE_Y }
	Indices for scaling factors in the x and y directions. More...
enum	e_complex_index { COMPLEX_RE , COMPLEX_IM }
	Indices for complex numbers (real and imaginary) More...
enum	e_number_flags { HAS_DIGIT , HAS_POINT }
	Flags for validating numbers. More...
enum	e_err_msg {   NO_TYPE , INVALID_TYPE , JULIA_ARGS , JULIA_NUM ,   MANDELBROT_ARGS }
	Error messages used for input validation. More...

Functions
void	calculate_scales_and_limits (t_render_vars *vars, t_data *data)
	Calculates scales and limits for rendering fractals.
int	precompute_coords (double **c_re, double **c_im, t_render_vars *vars)
	Precomputes coordinates for fractal rendering.
int	calculate_color (int iterations)
	Calculates the color based on the number of iterations.
double	ft_atod (const char *str)
	Converts a string to a double.
int	ft_strcmp (const char *s1, const char *s2)
	Compares two strings.
int	fr_putstr_fd (char *s, int fd)
	Writes a string to a file descriptor.
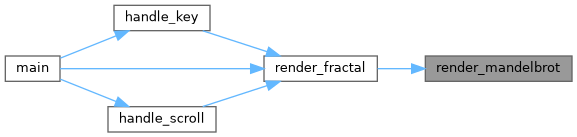
void	render_fractal (t_data *data)
	Render the specified fractal.
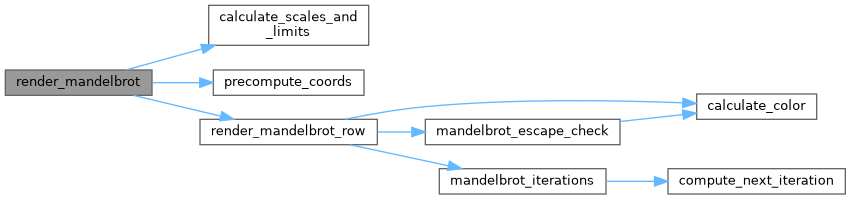
void	render_mandelbrot (t_data *data)
	Render the Mandelbrot fractal.
void	render_julia (t_data *data)
	Renders the Julia fractal.
void	handle_key (mlx_key_data_t keydata, void *param)
	Handles key inputs.
void	handle_scroll (double xdelta, double ydelta, void *param)
	Handles scroll inputs.

Macro Definition Documentation

FRACTAL_LIMIT

#define FRACTAL_LIMIT   4.0

Definition at line 192 of file fractol.h.

HEIGHT

#define HEIGHT   WIDTH

Definition at line 189 of file fractol.h.

LIGHT_GOLD

#define LIGHT_GOLD   "\033[38;5;220m"

Definition at line 196 of file fractol.h.

LIGHT_GREEN

#define LIGHT_GREEN   "\033[38;5;120m"

Definition at line 197 of file fractol.h.

LIGHT_RED

#define LIGHT_RED   "\033[38;5;203m"

Definition at line 195 of file fractol.h.

MAX_ITERATIONS

#define MAX_ITERATIONS   75

Definition at line 193 of file fractol.h.

RESET

#define RESET   "\033[0m"

Definition at line 194 of file fractol.h.

WIDTH

#define WIDTH   800

Definition at line 188 of file fractol.h.

ZOOM_IN

#define ZOOM_IN   1.1

Definition at line 190 of file fractol.h.

ZOOM_OUT

#define ZOOM_OUT   0.9

Definition at line 191 of file fractol.h.

Typedef Documentation

t_atod_data

typedef struct s_atod_data t_atod_data

Helper structure for string-to-double conversion.

t_color

typedef struct s_color t_color

Represents an RGB color.

t_complex_index

typedef enum e_complex_index t_complex_index

Indices for complex numbers (real and imaginary)

t_data

typedef struct s_data t_data

Data structure for fractal rendering.

t_fractal_type

typedef enum e_fractal_type t_fractal_type

t_number_flags

typedef enum e_number_flags t_number_flags

Flags for validating numbers.

t_offset_index

typedef enum e_offset_index t_offset_index

Indices for offsets in the x and y directions.

t_render_vars

typedef struct s_render_vars t_render_vars

Variables used for fractal rendering calculations.

t_scale_index

typedef enum e_scale_index t_scale_index

Indices for scaling factors in the x and y directions.

Enumeration Type Documentation

e_complex_index

enum e_complex_index

Indices for complex numbers (real and imaginary)

Enumerator
COMPLEX_RE
COMPLEX_IM

Definition at line 50 of file fractol.h.

{
    COMPLEX_RE,
    COMPLEX_IM,
}   t_complex_index;

e_err_msg

enum e_err_msg

Error messages used for input validation.

Enumerator
NO_TYPE
INVALID_TYPE
JULIA_ARGS
JULIA_NUM
MANDELBROT_ARGS

Definition at line 68 of file fractol.h.

{
    NO_TYPE,
    INVALID_TYPE,
    JULIA_ARGS,
    JULIA_NUM,
    MANDELBROT_ARGS,
};

e_fractal_type

enum e_fractal_type

Enumerator
MANDELBROT
JULIA

Definition at line 23 of file fractol.h.

{
    MANDELBROT,
    JULIA,
}   t_fractal_type;

e_number_flags

enum e_number_flags

Flags for validating numbers.

Enumerator
HAS_DIGIT
HAS_POINT

Definition at line 59 of file fractol.h.

{
    HAS_DIGIT,
    HAS_POINT,
}   t_number_flags;

e_offset_index

enum e_offset_index

Indices for offsets in the x and y directions.

Enumerator
OFFSET_X
OFFSET_Y

Definition at line 32 of file fractol.h.

{
    OFFSET_X,
    OFFSET_Y,
}   t_offset_index;

e_scale_index

enum e_scale_index

Indices for scaling factors in the x and y directions.

Enumerator
SCALE_X
SCALE_Y

Definition at line 41 of file fractol.h.

{
    SCALE_X,
    SCALE_Y,
}   t_scale_index;

Function Documentation

calculate_color()

int calculate_color

(

int

iterations

)

Calculates the color based on the number of iterations.

Calculates the color based on the number of iterations.

This function determines the color of each pixel in the fractal by mapping the iteration count (how many steps we are needed to reach a threshold) to a color gradient.

For non-technical users:

• The function decides the color of each pooint in the fractal, creating the beautiful patterns you see based on how "complex" the point is.

Parameters

iterations

Number of iterations required for the opint to "escape".

Returns

Returns the calculated color as an integer.

Definition at line 131 of file calcs.c.

{
    double  it_count;
    int     base_gray;
    t_color color;
 
    it_count = (double)iterations / MAX_ITERATIONS;
    base_gray = (30 + 190 * (it_count * (1 - 0.2 * it_count)));
    color.r = base_gray - (5 * (1 - it_count) * it_count * it_count);
    color.g = base_gray - (10 * (1 - it_count) * (1 - it_count));
    color.b = base_gray - (15 * (1 - it_count) * it_count);
    return ((0xFF << 24) | (color.r << 16) | (color.g << 8) | color.b);
}

Here is the caller graph for this function:

calculate_scales_and_limits()

void calculate_scales_and_limits	(	t_render_vars *	vars,
		t_data *	data
	)

Calculates scales and limits for rendering fractals.

Calculates scales and limits for rendering fractals.

This function determines how the fractal is scaled and positioned on the screen. It computes the scale factors for each pixel and establishes the starting points ffor the real and imaginary part of the fractal based on the zoom level and offsets.

For non-technical users:

• Think of it as setting the "zoom" and "pam" for the fractal to display it correctly on the screen.

Parameters

vars	Pointer to the rendering variables structure.
data	Pointer to the main data structure containing fractal information.

Definition at line 52 of file calcs.c.

{
    vars->scale[SCALE_X] = 4.0 / (WIDTH * data->zoom);
    vars->scale[SCALE_Y] = 4.0 / (HEIGHT * data->zoom);
    vars->start[COMPLEX_RE] = -2.0 / data->zoom + data->offset[OFFSET_X];
    vars->start[COMPLEX_IM] = -2.0 / data->zoom + data->offset[OFFSET_Y];
    vars->pixels = (uint32_t *)data->img->pixels;
}

Here is the caller graph for this function:

fr_putstr_fd()

int fr_putstr_fd	(	char *	s,
		int	fd
	)

Writes a string to a file descriptor.

Writes a string to a file descriptor.

Definition at line 109 of file utils.c.

{
    int i;
    int count;
 
    if (!s)
        return (0);
    i = 0;
    count = 0;
    while (s[i])
        count += write(fd, &s[i++], 1);
    return (count);
}

Here is the caller graph for this function:

ft_atod()

double ft_atod

(

const char *

str

)

Converts a string to a double.

Converts a string to a double.

Definition at line 19 of file utils.c.

{
    t_atod_data d;
 
    d.result = 0.0;
    d.fraction = 0.0;
    d.divisor = 10.0;
    d.sign = 1;
    d.i = 0;
    while (str[d.i] == 32 || (str[d.i] >= 9 && str[d.i] <= 13))
        d.i++;
    if (str[d.i] == '-' || str[d.i] == '+')
        if (str[d.i++] == '-')
            d.sign = -1;
    while (str[d.i] >= '0' && str[d.i] <= '9')
        d.result = d.result * 10.0 + (str[d.i++] - '0');
    if (str[d.i] == '.')
    {
        d.i++;
        while (str[d.i] >= '0' && str[d.i] <= '9')
        {
            d.fraction += (str[d.i] - '0') / d.divisor;
            d.divisor *= 10.0;
            d.i++;
        }
    }
    return (d.sign * (d.result + d.fraction));
}

Here is the caller graph for this function:

ft_strcmp()

int ft_strcmp	(	const char *	s1,
		const char *	s2
	)

Compares two strings.

Definition at line 51 of file utils.c.

{
    int i;
 
    i = 0;
    while (s1[i] == s2[i] && s1[i])
        i++;
    return (s1[i] - s2[i]);
}

Here is the caller graph for this function:

handle_key()

void handle_key	(	mlx_key_data_t	keydata,
		void *	param
	)

Handles key inputs.

Definition at line 64 of file utils.c.

{
    t_data  *data;
 
    data = (t_data *)param;
    if (keydata.key == MLX_KEY_ESCAPE)
        mlx_close_window(data->mlx);
    else if (keydata.key == MLX_KEY_W)
        data->offset[OFFSET_Y] -= 0.1 / data->zoom;
    else if (keydata.key == MLX_KEY_S)
        data->offset[OFFSET_Y] += 0.1 / data->zoom;
    else if (keydata.key == MLX_KEY_A)
        data->offset[OFFSET_X] -= 0.1 / data->zoom;
    else if (keydata.key == MLX_KEY_D)
        data->offset[OFFSET_X] += 0.1 / data->zoom;
    else if (keydata.key == MLX_KEY_UP)
        data->zoom *= ZOOM_IN;
    else if (keydata.key == MLX_KEY_DOWN)
        data->zoom *= ZOOM_OUT;
    if (data->zoom < 1e-5)
        data->zoom = 1e-5;
    render_fractal(data);
}

Here is the call graph for this function:

Here is the caller graph for this function:

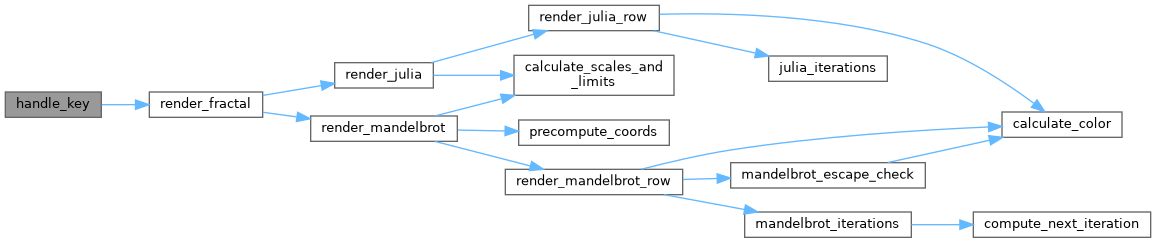
handle_scroll()

void handle_scroll	(	double	xdelta,
		double	ydelta,
		void *	param
	)

Handles scroll inputs.

Handles scroll inputs.

Definition at line 91 of file utils.c.

{
    t_data  *data;
 
    (void)xdelta;
    data = (t_data *)param;
    if (ydelta > 0)
        data->zoom *= ZOOM_IN;
    else
        data->zoom *= ZOOM_OUT;
    if (data->zoom < 1e-5)
        data->zoom = 1e-5;
    render_fractal(data);
}

Here is the call graph for this function:

Here is the caller graph for this function:

precompute_coords()

int precompute_coords	(	double **	c_re,
		double **	c_im,
		t_render_vars *	vars
	)

Precomputes coordinates for fractal rendering.

Precomputes coordinates for fractal rendering.

This function calculates the real and imaginary parts of the fractal for each pixel on the screen, storing them in arrays for quick access during rendering. It ensures that every point is prepared for the fractal calculations.

For non-technical users:

• Imagine this as creating a "grid" of points where the fractal will be drawn. This points tell the program where to caalculate the colors.

Parameters

c_re	Pointer to the array storing real coordinates.
c_im	Pointer to the array storing imaginary coordinates.
vars	Pointer to the rendering variables structure.

Returns

Returns 1 on success, or 0 if memory allocation fails.

Definition at line 78 of file calcs.c.

{
    int i;
 
    *c_re = (double *)malloc(WIDTH * sizeof(double));
    *c_im = (double *)malloc(HEIGHT * sizeof(double));
    if (!(*c_re) || !(*c_im))
        return (free(*c_re), free(*c_im), 0);
    i = -1;
    while (++i < WIDTH)
        (*c_re)[i] = vars->start[COMPLEX_RE] + i * vars->scale[SCALE_X];
    i = -1;
    while (++i < HEIGHT)
        (*c_im)[i] = vars->start[COMPLEX_IM] + i * vars->scale[SCALE_Y];
    return (1);
}

Here is the caller graph for this function:

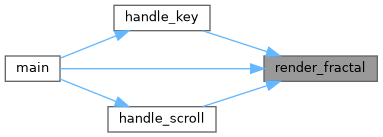
render_fractal()

void render_fractal

(

t_data *

data

)

Render the specified fractal.

Render the specified fractal.

This function selects the appropiate rendering algorithm based on the fractal type chosen by the user (Julia or Mandelbrot) and renders it on the screen.

For non-technical users:

• Depending on the type of fractal (Julia or Mandelbrot), this function draws the chosen fractal pattern for you to see.

Parameters

data	Pointer to the main data structure containing fractal and rendering details.

Definition at line 108 of file calcs.c.

{
    if (data->fractal_type == JULIA)
        render_julia(data);
    else if (data->fractal_type == MANDELBROT)
        render_mandelbrot(data);
}

Here is the call graph for this function:

Here is the caller graph for this function:

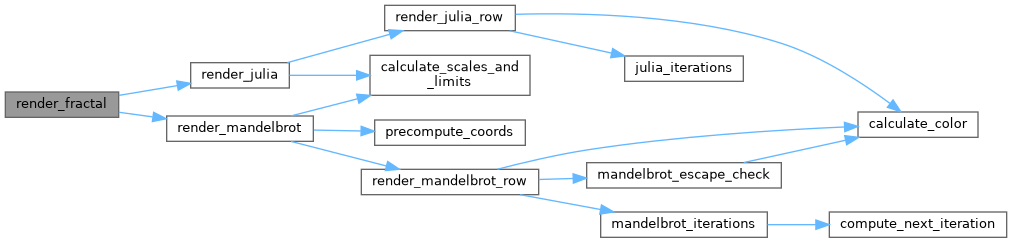
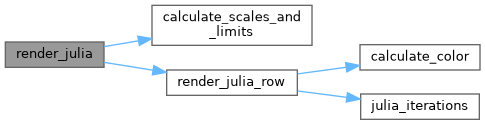
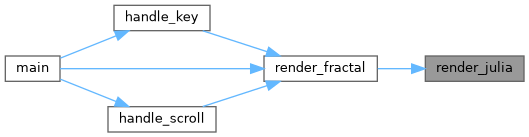
render_julia()

void render_julia

(

t_data *

data

)

Renders the Julia fractal.

Renders the Julia fractal.

This function handles the full rendering process for the Julia set by iterating through all rows of the screen, rendering each row sequentially.

• Setup:
  • Calculates the scaling and starting coordinates based on the zoom level and positional offsets provided by the user.
• Row-by-Row Rendering:
  • For each row on the screen (y coordinate), the corresponding imaginary coordinate is computed.
  • The row is passed to render_julia_row, which handles the pixel-by-pixel rendering.
• Full Image Construction:
  • The ffunction processes every row until the entire fractal is rendered.

Parameters

data	Pointer to the main fractal data structure, including rendering details such as zoom, offsets, and fractal paarameters.

Definition at line 165 of file julia.c.

{
    t_render_vars   vars;
    int             y;
 
    calculate_scales_and_limits(&vars, data);
    y = 0;
    while (y < HEIGHT)
    {
        vars.c_im = vars.start[COMPLEX_IM] + y * vars.scale[SCALE_Y];
        render_julia_row(&vars, data, y++);
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

render_mandelbrot()

void render_mandelbrot

(

t_data *

data

)

Render the Mandelbrot fractal.

Render the Mandelbrot fractal.

Definition at line 151 of file mandelbrot.c.

{
    t_render_vars   vars;
    double          *precomputed_c_re;
    double          *precomputed_c_im;
    int             y;
 
    calculate_scales_and_limits(&vars, data);
    if (!precompute_coords(&precomputed_c_re, &precomputed_c_im, &vars))
        return ;
    y = 0;
    while (y < HEIGHT)
    {
        vars.c_im = precomputed_c_im[y];
        render_mandelbrot_row(&vars, data, y++);
    }
    free(precomputed_c_re);
    free(precomputed_c_im);
}

Here is the call graph for this function:

Here is the caller graph for this function: